Orthorhombic

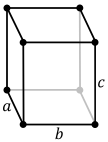
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.

Bravais latticesEdit

Further information: Bravais lattice

Rectangular vs rhombic unit cells for the 2D orthorhombic lattices. The swapping of centering type when the unit cell is changed also applies for the 3D orthorhombic lattices

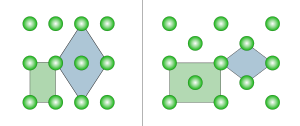
Two-dimensionalEdit

In two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular. The primitive rectangular lattice can also be described by a centered rhombic unit cell, while the centered rectangular lattice can also be described by a primitive rhombic unit cell.

Three-dimensionalEdit

In three dimensions, there are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.

Bravais lattice	Primitive orthorhombic	Base-centered orthorhombic	Body-centered orthorhombic	Face-centered orthorhombic
Pearson symbol	oP	oS	oI	oF
Standard unit cell
Right rhombic prism unit cell

In the orthorhombic system there is a rarely used second choice of crystal axes that results in a unit cell with the shape of a right rhombic prism;^[1] it can be constructed because the rectangular two-dimensional base layer can also be described with rhombic axes. In this axis setting, the primitive and base-centered lattices swap in centering type, while the same thing happens with the body-centered and face-centered lattices. Note that the length ${\displaystyle a}$ in the lower row is not the same as in the upper row, as can be seen in the figure in the section on two-dimensional lattices. For the first and third column above, ${\displaystyle a}$ of the second row equals ${\displaystyle {\sqrt {a^{2}+b^{2}}}}$ of the first row, and for the second and fourth column it equals half of this.

Crystal classesEdit

The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,^[2] orbifold notation, type, and space groups are listed in the table below.

№	Point group					Type	Example	Space groups
	Name[3]	Schön.	Intl	Orb.	Cox.			Primitive	Base-centered	Face-centered	Body-centered
16–24	Rhombic disphenoidal	D2 (V)	222	222	[2,2]+	Enantiomorphic	Epsomite	P222, P2221, P21212, P212121	C2221, C222	F222	I222, I212121
25–46	Rhombic pyramidal	C2v	mm2	*22	[2]	Polar	Hemimorphite, bertrandite	Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2	Cmm2, Cmc21, Ccc2 Amm2, Aem2, Ama2, Aea2	Fmm2, Fdd2	Imm2, Iba2, Ima2
47–74	Rhombic dipyramidal	D2h (Vh)	mmm	*222	[2,2]	Centrosymmetric	Olivine, aragonite, marcasite	Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma	Cmcm, Cmca, Cmmm, Cccm, Cmme, Ccce	Fmmm, Fddd	Immm, Ibam, Ibca, Imma

This article uses material from the Wikipedia article  Metasyntactic variable, which is released under the  Creative Commons Attribution-ShareAlike 3.0 Unported License.